Lógica Difusa

LÓGICA DIFUSA

“El modelo de la lógica difusa es la mente humana” (Lofti Zadeh)

“La esencia de la lógica difusa es que todo es cuestión de grado, incluyendo la noción de pertenencia” (Lofti Zadeh)

“Los opuestos son idénticos en naturaleza, pero diferentes en grado” (El Kybalion)

Lógica Difusa
La lógica difusa o borrosa (fuzzy logic) fue propuesta por primera vez por Lofti Zadeh (profesor de la Universidad de Berkeley) en su famoso artículo de 1965 titulado “fuzzy Sets” [Zadeh, 1965] que revolucionó el pensamiento lógico tradicional. Sus principios y características son los siguientes:

Se basa en conceptos borrosos, difusos, que son de tipo cualitativo, como alto, bajo, rico, pobre, joven, viejo, frío, caliente, rápido, lento, etc. Los conceptos “verdadero” y “falso” también son difusos. Estos conceptos difusos se estructuran como variables cualitativas y valores cualitativos. Por ejemplo, la variable “edad” y sus posibles valores cualitativos son: muy joven, joven, maduro, viejo, muy viejo.

Lo difuso, borroso o aproximado (fuzzy) es lo opuesto a exacto, preciso o nítido (crisp). Según Zadeh, la lógica difusa es el modelo de la mente humana, por lo que es fácil de entender y usar.
Es una generalización de la lógica clásica, booleana o bivalente. También es una generalización de la lógica infinito−valente basada en valores de verdad entre 0 (falso) y 1 (verdadero), en la que estos valores son complementarios (suman 1). En la lógica difusa, los valores verdadero (V) y falso (F) son independientes y pueden no sumar 1. Un concepto o propiedad difuso puede ser a la vez parcialmente V y parcialmente F. Por ejemplo, una persona puede no ser ni alta ni baja, sino participar a la vez de ambas propiedades en cierto grado. Solo cuando su altura está por encima de un cierto valor, es completamente alta y no baja. Y cuando está por debajo de otro cierto valor, se considera completamente baja y no alta.
El principio principal borroso es que nada es absoluto, que “Todo es cuestión de grado”. Un ejemplo clásico que suele ponerse es el siguiente: “¿Cuántos granos de arena constituyen un montón?”. Si empezamos desde cero, añadiendo un grano cada vez, en algún momento podría ser calificado como montón. Una vez creado el montón, si quitamos un grano, ¿sigue siendo un montón? Los límites del concepto “montón” son difusos.
Permite resolver el problema de las paradojas lógicas. El problema del montón es un ejemplo de paradoja. Las paradojas lógicas aparecen con la bivalencia de valores de verdad (verdadero y falso) cuando una sentencia es a la vez verdadera y falsa. Las paradojas desaparecen cuando se consideran grados de verdad.
Como toda lógica polivalente, la lógica difusa rompe también la dicotomía de la lógica aristotélica y las dos leyes aristotélicas: 1) la ley de no contradicción: A no puede ser a la vez B y no-B; 2) ley de tercero excluido (tertium non datur): A debe ser B o no-B. Estas dos leyes han constituido el fundamento de la lógica durante 2000 años.
Permite representar la información imprecisa y parcial, de manera flexible y fácilmente modificable. También permite representar fácilmente el conocimiento para aplicaciones de inteligencia artificial. El conocimiento se representa de manera compacta y modular mediante un conjunto de reglas que son relaciones lógicas entre variables cualitativas, que permiten el razonamiento cualitativo o aproximado. Las reglas son de tipo heurístico, en lugar de reglas detalladas, de “fuerza bruta”. Por ejemplo, en juegos de estrategia (como el ajedrez), en vez de considerar todas las posibles jugadas en detalle, se puede representar el conocimiento en forma de estrategias generales, de patrones, etc. Esto supone un nivel superior de conocimiento, por lo que se mejora el rendimiento y la efectividad.
Es muy adecuada para las llamadas “ciencias blandas”, como la lingüística, la psicología, la sociología, la economía, la política, etc. Pero también es útil para las técnicas (informática, electrónica, inteligencia artificial, etc.) e incluso para las teóricas (matemática, lógica, teoría de la información, filosofía, etc.).

Operaciones lógicas

Si representamos, en general, con C(x) el grado de verdad de x respecto a un concepto C, tenemos las definiciones siguientes:

Contraria lógica difusa: 1−C(x)
Suma lógica difusa:
max(C(x), C(y))
Producto lógico difuso:
min(C(x), C(y))

La implicación lógica C(x)→C(y) admite muchas interpretaciones, existiendo diferentes modelos, que toman el nombre de sus proponentes. Destacamos las siguientes:

Implicación de Lucasiewicz.
Se basa en la equivalencia p→q ≡ ¬p∨q de la lógica bivalente. Por lo tanto, equivale a max(1−C(x), C(y)).
Implicación de Gódel.
C(x)→C(y) = 1 si C(x)≤C(y), C(y) en caso contrario.
Implicación de Sharp.
C(x)→C(y) = 1 si C(x)≤C(y), 0 en caso contrario.
Implicación de Mamdani. C(x)→C(y) = min(C(x), C(y)).

Conjuntos Difusos
La idea tras un conjunto difuso es muy simple. En la teoría clásica de conjuntos de Cantor, los elementos pertenecen o no pertenecen a los conjuntos. En la teoría de conjuntos difusos, un elemento puede pertenecer parcialmente a un conjunto:

Para todo elemento x, su grado de pertenencia a un conjunto C está definido por una función f(x). El valor 1 de la función se interpreta como que x pertenece a C (x∈C), y el valor 0 como que x no pertenece a C (x∉C). Esta es la concepción clásica en teoría de conjuntos. Pero si esta función toma valores entre 0 y 1, estos valores indican el grado de pertenencia al conjunto y C es un conjunto difuso.

La formalización de los conjuntos difusos la realizó Zadeh en su artículo de 1965 en el que creó un sistema axiomático generalizado de la teoría de conjuntos basado en el concepto de pertenencia parcial.

Definiciones formales

Un conjunto difuso A, en el universo del discurso X, es un conjunto de pares ordenados (x, μ_A(x)), siendo μ_A(x) la función de pertenencia de x al conjunto A.
Un conjunto difuso A es un subconjunto de un conjunto difuso B si μ_A(x)≤ μ_B(x) para todo x∈A.
El soporte de un conjunto difuso A es el conjunto de los elementos que tienen un grado de pertenencia a A. Si el soporte es ∅, se denomina conjunto difuso vacío. Si el soporte es un solo elemento, se denomina singleton difuso.
La altura de un conjunto difuso es el mayor valor de su función de pertenencia.
El núcleo de un conjunto difuso es el conjunto de elementos que pertenecen al conjunto con grado 1.
La cardinalidad de un conjunto difuso A, en el universo del discurso X, es:
El alfa−corte (α-corte) de un conjunto difuso A es el conjunto de los elementos que tienen un grado de pertenencia a A igual o superior a α. Un conjunto difuso se puede descomponer en una familia de conjuntos difusos mediante α-cortes.

Operaciones con conjuntos difusos

Si representamos, en general, con C(x) el grado de pertenencia de x en C, tenemos las definiciones siguientes:

Conjunto complementario de un conjunto A: A^C(x) = (1−A(x))
Unión de conjuntos: (A∪B)(x) = max[A(x), B(x)]
Intersección de conjuntos: (A∩B)(x) = min[A(x), B(x)]

Números difusos

Zadeh propuso el concepto de número difuso (fuzzy number) como un caso especial de conjunto difuso. Así como la lógica difusa es una extensión de la lógica booleana, y los conjuntos difusos son una extensión de los conjuntos tradicionales, los números difusos son una extensión de los números reales.

Un número difuso es una extensión de un número real en el sentido de que no se refiere a un solo valor, sino a un conjunto de valores, cada uno con su correspondiente “peso”, factor o grado de pertenencia (un valor entre 0 y 1) a la recta real. El conjunto es convexo, es decir, que el conjunto de valores no tiene “huecos”, forman un continuo, que puede ser toda la recta real o un intervalo de la misma. En general, un número difuso es un segmento finito o infinito de la recta real, cuyos elementos tiene un grado de pertenencia a la recta real.

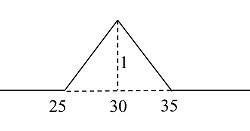
Un ejemplo de número difuso sobre toda la recta real es el número triangular siguiente:

Un número difuso se puede considerar una función entre los números de un segmento de la recta real y los números entre 0 y 1. En el ejemplo, el grado de pertenencia entre 25 y 30 se incrementa de forma lineal entre 0 y 1, y luego decrementa (también de forma lineal) entre 30 y 35 entre 1 y 0.

Un número real es un caso particular de número difuso: es un segmento reducido a un solo punto que representa un número real con grado de pertenencia 1.

Las operaciones aritméticas difusas sobre los números difusos son las mismas que las operaciones con conjuntos: complementario, suma y producto.

Variables lingüísticas

Zadeh introdujo en 1973 el concepto de “variable lingüística” en la que establecía una equivalencia entre variable y conjunto difuso.

Una variable numérica (p.e. “edad”) toma un valor cuantitativo (numérico) concreto (p.e. edad=43). Una variable lingüística tiene un conjunto de valores lingüísticos, cualitativos (o categorías) posibles, por ejemplo,

{muy joven, joven, mediana edad, viejo, muy viejo} La granularidad de una variable lingüística es el número de valores cualitativos que se definen para ella. En el ejemplo, la granularidad de edad es 5. Una granularidad fina indica muchos valores cualitativos. Una granularidad gruesa indica pocos valores cualitativos.

Hay una función que, para cada edad, asigna un valor numérico (entre 0 y 1) a cada uno de estos valores cualitativos, que indica el grado de pertenencia a esas categorías. El resultado es un conjunto. Por ejemplo,

edad=30 → {(0, muy joven), (0.4, joven), (0.6, mediana edad), (0, viejo), (0, muy viejo)} Los valores lógicos “verdadero” y “falso” son valores cualitativos de la variable lingüística “verdad”.

Antecedentes

Platón fue el primero en cuestionar la lógica bivalente al afirmar: “Hay una tercera región entre lo verdadero y lo falso donde los opuestos se presentan juntos”.
Aristóteles, discípulo de Platón, también puso en cuestión el principio de bivalencia: “En algunos casos hay eventualidad y de la afirmación y la negación ninguna es mas verdadera que la otra” (De interpretatione).
Charles Sanders Peirce estaba en desacuerdo con Cantor en caracterizar las cosas como pertenecientes o no a conjuntos. Decía que todas las cosas existen sobre un continuo.
Vasiliev, en 1909, desarrolló una lógica trivalente y eliminando el principio del tercero excluido de la lógica clásica, pero no llegó a formalizarla totalmente.
Jan Lukasiewicz propuso en su artículo de 1920 “On three-valued logic”, la idea de que la dicotomía lógica verdadero−falso habría que ampliarla con un tercer valor interpretado como “indeterminado” o “incierto”, de valor ½ (intermedio entre 0 y 1), creando así la lógica trivalente. Posteriormente, en 1970, afirmó que podía asignarse cualquier valor intermedio entre 0 (falso) y 1 (verdadero), que representaría el “grado de verdad”. Lukasiewicz es considerado el creador de la lógica polivalente y la lógica infinitovalente.
Bertrand Russell creía que la vaguedad era una característica del lenguaje humano, pero no de la realidad. Publicó en 1973 el artículo “La vaguedad” en el que se preguntaba cuantos pelos ha de perder una persona para ser considerada calva.
Finalmente, Lofty Zadeh, en 1965 −inspirado en la idea de pertenencia difusa a un conjunto− propuso la idea de la “lógica difusa” (fuzzy logic), una lógica de infinitos valores, asociados a los valores “verdadero” y “falso” (independientes entre sí) y a conceptos difusos en general.

Borrosidad vs. probabilidad

Borrosidad y probabilidad (o aleatoriedad) son conceptos distintos. Hay muchas diferencias conceptuales y teóricas entre ambos. Hay también similaridades, siendo la principal que ambos describen incertidumbres, con números asociados entre 0 y 1.

La lógica difusa y la probabilidad expresan tipos de incertidumbre diferentes. La aleatoriedad es un tipo de incertidumbre, pero no es difusa. La borrosidad es un tipo de incertidumbre, pero no es aleatoria.
La aleatoriedad describe la incertidumbre de que ocurra un cierto evento futuro, que puede ocurrir o no. La lógica difusa mide o describe la ambigüedad o borrosidad de sucesos que ya han ocurrido, asignando valores (entre 0 y 1) a los elementos de un conjunto.

Si un evento ocurre o no es aleatoriedad. En qué grado ocurre es borrosidad. Si todos los eventos son nítidos, no hay borrosidad, solo hay aleatoriedad. La borrosidad es una propiedad o atributo de un suceso.
La probabilidad es objetiva, y es función de la información disponible. Se puede calcular a nivel teórico y se puede verificar en la práctica. Lo difuso es subjetivo.
La probabilidad de los posibles sucesos siempre suman 1. En lógica difusa, la suma de los grados asignados a los diferentes valores cualitativos o categorías de un concepto no tienen por qué sumar 1. Por ejemplo, a una estatura determinada (p.e. 1.70) se le pueden asociar los valores {0.1×alto, 0.3×bajo, 0.8×normal}, cuyos grados no suman 1. Y a una figura irregular se le puede asociar {0.8×círculo, 0.3×cuadrado}, cuyos grados tampoco suman 1.
Con el aumento de información (los casos posibles), la probabilidad se hace más precisa y la borrosidad aumenta.

Soft Computing

Según Zadeh, la lógica difusa no es una disciplina aislada, sino que forma parte de lo que denomina “Soft Computing” (en español, “computación blanda”). Sus características son:

Estudia y modeliza fenómenos complejos que por los métodos tradicionales matemático−analíticos (análisis numérico, lógica proposicional, lógica de predicados, etc.) son insuficientes o requieren un gran consumo de recursos para obtener una solución que a veces es incompleta o imprecisa. Los sistemas complejos aparecen en biología, ciencias sociales, medicina, etc. Paradójicamente, utiliza modelos analíticos simplificados para capturar la complejidad.
Tolera la imprecisión, la incertidumbre y la verdad parcial. Utiliza razonamiento difuso, aproximado, probabilístico y heurístico. Este modelo es el de la mente humana. En este aspecto difiere de la computación “hard” (como por ejemplo, la investigación operativa).
Engloba principalmente la lógica difusa, las redes neuronales y la computación evolutiva (algoritmos genéticos, algoritmos evolutivos). Otras técnicas que utiliza son: razonamiento probabilístico, teoría del caos, teoría del aprendizaje, teoría de conjuntos aproximados (rough set theory), inteligencia grupal (swarm intelligence), redes de propagación de creencias, teoría de la posibilidad, análisis “blando” de datos (soft data), búsquedas especiales (tabú, reactivas y armónicas), heurísticas y meta−heurísticas (evolutivas y de relajación), etc. Se denomina “relajación” de un problema cuando se llega un momento en que éste se simplifica debido a la modificación o debilitamiento de algunos elementos del problema.

Un rough set (conjunto aproximado) es una aproximación formal de un conjunto convencional mediante un par de conjuntos que proporcionan la aproximación superior e inferior del conjunto. Estas dos aproximaciones pueden ser conjuntos convencionales o difusos.

El programa BISC (The Berkeley Iniciative in Soft Computing) es una iniciativa de Lofti Zadeh orientada al estudio y desarrollo del Soft Computing.

Sistemas de control difusos

Las ideas básicas del control lógico difuso (fuzzy logic control) las proporcionó Zadeh [1972]. Se trata del diseño de sistemas de control mediante un conjunto de reglas difusas, que tienen, en general, la forma

₁

₂

₁

₂

siendo x₁, x₂,... las variables cualitativas de entrada, y v₁, v₂,... los valores correspondientes a cada una de estas variables. Análogamente para las variables cualitativas de salida y sus valores (y₁, y₂, ... y w₁, w₂, ...). También pueden aparecer en el antecedente expresiones del tipo “x_i no es v_i” y el operador “o” (disyunción lógica) en lugar de “y” (conjunción lógica).

Cada regla tiene un “peso” o importancia, que es un valor numérico.

La ventaja de las reglas difusas es que son de tipo conceptual, por lo que son fáciles de interpretar, pues representan el conocimiento a nivel cualitativo exclusivamente. El razonamiento se realiza a nivel cualitativo. Una vez obtenidos los resultados cualitativos, estos se transforman en cuantitativos.

Las reglas de un modelo difuso que hay que contrastarlas en la práctica. Las reglas se van refinando hasta obtener finalmente un modelado satisfactorio.

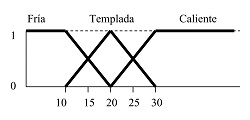
Un ejemplo simple ilustrativo es un sistema de control para regular un ventilador. En este caso solo hay una variable de entrada, la temperatura ambiente t, y una variable de salida w, la velocidad angular (en r.p.m) del ventilador. Se contemplan 3 valores cualitativos para la temperatura: Fría, Templada y Caliente, definidas según este gráfico:

La velocidad angular w tiene asociadas 3 valores cualitativos: Mínima, Media y Máxima. En este caso, cada uno de estos valores cualitativos tiene asignado un valor cuantitativo: w₁, w₂, w₃, que corresponden al valor medio o de referencia de la velocidad angular.

Las reglas difusas son, en este caso, muy simples:

En este caso, los pesos de las reglas son todas la unidad, es decir, todas tienen el mismo peso.

La operativa de un sistema de control difuso consta de 3 fases:

Fuzzificación de los valores de entrada.
También llamada de clasificación difusa, convierte los valores de entrada cuantitativos en cualitativos a través de un elemento fuzzificador o clasificador difuso.
En este caso, la temperatura de entrada t se convierte en 3 valores difusos: f₁×Fría, f₂×Templada y f₃×Caliente.
Evaluación de las reglas difusas del sistema.
Se evalúan todas las reglas y se disparan o activan las reglas que cumplen las condiciones. Por ejemplo, si f₁=0, f₂=0.5 y f₃=0.7, se disparan las reglas R2 y R3, obteniéndose los valores cualitativos de salida correspondientes. En este caso, Media y Máxima.
Desfuzzificación.
A partir de los pesos de las reglas disparadas y de los valores cuantitativos asociados a los valores cualitativos de salida, una función calcula el valor numérico de salida de w, la velocidad angular del ventilador. Este proceso se realiza mediante un elemento desfuzzificador, desclasificador difuso.

Existen muchas técnicas de desfuzzyficación, que combinan de diferentes formas estos valores para obtener la salida. El sistema más utilizado es el del “centro de gravedad” (o centroide). En el caso del ventilador,

Cuantificadores difusos

Uno de los aspectos más importantes de la lógica difusa es que permite extender y formalizar el concepto de cuantificación, interpretado como subconjunto difuso. Este tema fue también introducido por Zadeh [1983].

Un cuantificador nítido o preciso es un número concreto. Un cuantificador difuso (o lingüístico) permite expresar una cantidad de una manera cualitativa, difusa, aproximada. Parece algo paradójico que cantidad y cualidad, que son conceptos diferentes, se unan en este concepto de cuantificador difuso para expresar una cantidad mediante una cualidad. Pero los cuantificadores difusos son esenciales para la comunicación efectiva en el lenguaje natural.

Los cuantificadores difusos pueden ser de dos tipos: absolutos y relativos.

Cuantificador absoluto.
Un cuantificador absoluto expresa una cantidad (de forma cualitativa) sobre el número total de elementos de un determinado conjunto C. Por ejemplo: entre 5 y 10, más de 10, al menos 2, aproximadamente 8, muchos más que 100, etc.

Los cuantificadores difusos absolutos se definen como conjuntos difusos en la recta real positiva, es decir, en el intervalo (0, ∞), es decir, como un número difuso definido en ese intervalo.
Cuantificador relativo.
Un cuantificador relativo (o proporcional) expresa también una cantidad sobre el número total de elementos de un determinado conjunto −como en el caso de los cuantificadores absolutos−, pero la expresa mediante una proporción respecto al conjunto completo. Por ejemplo, la mayoría, la minoría, algunos, aproximadamente la mitad, casi ninguno, al menos la tercera parte, casi todos, etc.

Los cuantificadores difusos relativos se definen como conjuntos difusos en el segmento [0, 1] de la recta real, es decir, como un número difuso definido en ese intervalo. Para evaluar un cuantificador relativo se necesitan dos cantidades: el número de elementos del conjunto original C y el número de elementos correspondientes al subconjunto seleccionado D . El resultado es también un número entre 0 y 1.

Los cuantificadores son, pues, funciones Q(φ) entre φ y [0, 1], siendo φ el número de elementos (en el caso del cuantificador absoluto) o una proporción (en el caso del cuantificador relativo). Si Q(φ) = 1, el cuantificador se satisface plenamente. Si Q(φ) = 0, el cuantificador no se satisface en absoluto. Un valor intermedio (entre 0 y 1) indica el grado de cumplimiento del cuantificador, es decir, el grado de pertenencia al conjunto difuso.

Hay cuantificadores crecientes. Por ejemplo:

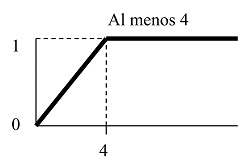
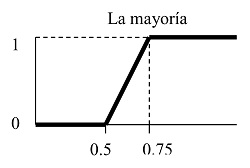
Y cuantificadores decrecientes. Por ejemplo:

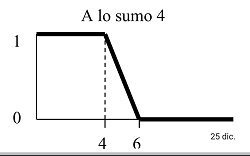
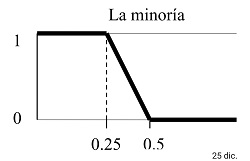
Los cuantificadores unimodales son los que tienen una función de pertenencia que es primero creciente y luego decreciente. Por ejemplo (el primero es absoluto y el segundo es relativo):

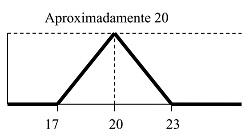
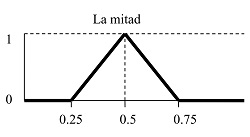
En lógica matemática solo hay dos cuantificadores: el cuantificador universal (“todos los elementos”, ∀) y el cuantificador existencial (“al menos un elemento”, ∃). Se les puede considerar como casos particulares de cuantificadores difusos:

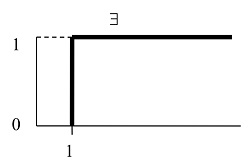
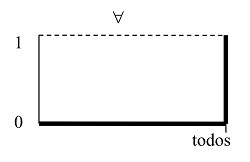
Bart Kosko: el Pensamiento Difuso
Bart Kosko es un notable investigador y defensor de la lógica difusa, a la que ha relacionado con la filosofía de la mente. Ha contribuido en gran manera a popularizarla. Su libro más conocido es “fuzzy Thinking” [Kosko, 1994]. Kosko es un converso total a la doctrina difusa, más radical incluso que el propio Zadeh.

En el concepto de verdad, Kosko resalta las diferencias entre la filosofía occidental frente a la filosofía oriental y que resume en la oposición entre Buda y Aristóteles (Buda murió 100 años antes de que naciera Aristóteles):

Aristóteles	Buda
A o no-A	A y no-A
Todo o nada	Un grado
Exacto	Difuso
Discreto: 0 o 1	Continuo: entre 0 y 1
Lenguaje formal	Lenguaje natural
Bit (binary digit)	Fit (fuzzy unit)

Un bit es un dígito binario (0 o 1). Un fit es un grado, un valor entre 0 y 1.

La filosofía occidental, heredera de Aristóteles, aceptó la bivalencia como una forma de simplificación de una realidad compleja. Esta filosofía ha permitido notables avances en ciencia, pero es una filosofía incompleta, parcial. En cambio, la filosofía oriental acepta la unión de los opuestos, el equilibrio de los principios universales del yin y el yang.

Kosko realizó varias aportaciones notables a este tema, entre ellas: el concepto de “fit” (el grado de pertenencia o borrosidad), la visión geométrica de los conjuntos difusos, la delimitación conceptual clara entre probabilidad y borrosidad, los subconjuntos difusos y la entropía difusa.

La visión geométrica de los conjuntos difusos

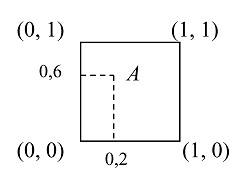
Si tenemos el conjunto X={x₁, x₂}, sus 2² = 4 subconjuntos son: ∅, {x₁}, {x₂}, {x₁,x₂}. Estos subconjuntos se pueden representar mediante cadenas de bits (mensajes bivalentes), en donde cada bit (0 o 1) indica no-pertenencia y pertenencia al conjunto X, respectivamente: (0, 0), (1, 0), (0, 1), (1, 1). En un sistema gráfico cartesiano bidimensional, estos subconjuntos están en los vértices de un cuadrado (ver figura). En general, para un conjunto de n elementos, los 2ⁿ subconjuntos están en los vértices en un hipercubo de dimensión n.

Un subconjunto difuso, por ejemplo, A=(0.2, 0.6), es un punto dentro del cuadrado. El conjunto de todos los subconjuntos difusos son todos los puntos del cuadrado excepto los 4 vértices, que corresponden a subconjuntos nítidos (no difusos).

El conjunto complementario de A es el complementario a 1 de sus componentes: A^C = (0.8, 0.4), de tal manera que:

A∪A^C = (0.8, 0.6) ≠ X (no se cumple el principio del tercero excluido)
A∩A^C = (0.2, 0.4) ≠ ∅ (no se cumple el principio de no-contradicción)

Un subconjunto A es difuso si y solo si A∪A^C ≠ X y A∩A^C ≠ ∅.

Un subconjunto A es nítido si y solo si A∪A^C = X y A∩A^C = ∅.

Los puntos correspondientes a los conjuntos A, A^C, A∪A^C y A∩A^C forman los vértices de un cuadrado interior al cuadrado original (ver figura).

El punto medio del cuadrado M = (0.5, 0.5) es un punto especial. Corresponde al conjunto más difuso de todos, pues cumple M∪M^C = M∩M^C = M = M^C. Es un punto equidistante de los 4 vértices del cuadrado, y es equivalente a la metáfora de la botella medio llena y medio vacía, que es donde aparecen las paradojas.

La cardinalidad de un conjunto A, representado como |A|, es la suma de sus valores fit:

Si consideramos que A es la probabilidad de que una variable aleatoria tenga un valor en el rectángulo formado por los vértices (0, 0) y A, se cumple:

Subconjuntividad

El grado de inclusión o subconjuntividad (subsethood) s de un conjunto A en otro B es un fit definido como:

Esta expresión recuerda a la fórmula de la probabilidad (bayesiana) de un suceso B condicionado a un suceso A:

Si A=(0.3, 0.3) y B=(0.5, 0.5), entonces s(A, B) = (0.3 + 0.3)/0.6 = 1.

Si A=(0.5, 0.5) y B=(0.3, 0.3), entonces s(A, B) = (0.3 + 0.3)/1 = 0.6.

Entropía borrosa

Según Kosko, la entropía es un concepto general; no está ligada forzosamente a la teoría de la probabilidad. La entropía mide la incertidumbre de un sistema o mensaje.

Kosko introdujo el concepto de “entropía borrosa”, que sirve para medir el grado de borrosidad de un conjunto.

La entropía de A −simbolizado por E(A)−, es el grado en que A∪A^C es un subconjunto de A∩A^C, es decir, el grado en que el todo está incluido en la parte, el grado de violación de la ley de no−contradicción respecto a la ley del tercero excluido:

En el caso del conjunto A=(0.2, 0.6), se tiene: E(A)= 0.6/1.4 = 0.42

La entropía de los vértices (subconjuntos nítidos) es 0, que es la mínima entropía. Si A=A^C (punto central), entonces E(A)=1, que es la máxima entropía. A medida que nos aproximamos al centro, la entropía crece y en el centro se obtiene la máxima entropía.

MENTAL: La Generalización de lo Difuso
Universalismo difuso y lingüística

La teoría difusa tiene una orientación universal, reflejada en su principio “Todo es cuestión de grado”. Se habla de conjuntos difusos, lógica difusa, números difusos, operaciones difusas, reglas difusas, algoritmos difusos, etc. Pero esa universalidad en la práctica es muy difícil de lograr por la falta de un lenguaje formal común.

MENTAL aporta un modelo lingüístico sobre un marco conceptual común y una teoría−práctica universal que permite expresar todo tipo de expresiones difusas como: matrices difusas, secuencias difusas, vectores difusos, ecuaciones difusas, predicados difusos, algoritmos difusos, etc. Y toda disciplina puede ser formalizada de forma difusa: aritmética difusa, geometría difusa, álgebra difusa, etc. Esa universalidad de MENTAL proporciona un marco integrador de las técnicas de Soft Computing.

MENTAL es un modelo de la mente que integra los dos modos de conciencia, los asociados a los hemisferios cerebrales. La visión aristotélica (del hemisferio izquierdo, HI) y la visión budista (del hemisferio derecho, HD), la integración entre lo preciso y lo difuso, entre lo cuantitativo y lo cualitativo, entre discreto y lo continuo, entre lo digital y lo analógico, entre lo superficial y lo profundo, entre lo analítico y lo sintético, entre la teoría y la práctica, entre lo particular y lo universal, etc. Lo que Kosko denomina “Aristóteles vs. Buda” es, pues, realmente la dicotomía o dualidad HI−HD.

Lo nítido o preciso es un caso particular de lo difuso. Lo difuso es lo universal. Lo nítido o preciso es lo particular.

La teoría difusa intenta humanizar la lógica y la matemática acercando lo formal a lo conceptual o mental. Pero la humanización completa se logra con MENTAL y sus primitivas semánticas universales.

Expresiones factorizadas

En MENTAL, toda expresión del tipo que sea (conjunto, secuencia, función, regla, procedimiento, vector, matriz, valor de verdad (V), cualidad, etc.), puede estar afectada por un factor. Hay 3 tipos de expresiones factorizadas:

Expresiones nítidas o precisas. Son expresiones en las que no intervienen valores cualitativos. Corresponden al modo de conciencia analítico. Por ejemplo,
Expresiones difusas. Son valores cualitativos de variables lingüísticas. Corresponden al modo de conciencia sintético. Por ejemplo: alto, rico, rápido, joven, etc.
Expresiones mixtas. Son del tipo f*x, siendo f un factor entre 0 y 1, y x un valor cualitativo, Por ejemplo, 0.7*alto, 0.3*joven, etc. Corresponden a la unión de los dos modos de conciencia (HI y HD), donde se unen lo cualitativo y lo cuantitativo, lo preciso y lo difuso. Esto es precisamente lo que ha hecho la lógica difusa y que justifica que se la considere un modelo de la mente humana.

Magnitudes cuantitativas y cualitativas

Las magnitudes son de la forma r*x, en donde r es un número real y x es una unidad de medida o un valor cualitativo.

Si el factor r es mayor que 1 y x es una unidad de medida, tenemos una magnitud cuantitativa. Por ejemplo, en magnitudes como peso, altura, en donde hay una unidad de medida.


17*Kg    23*m    80*(Km÷h)

Si r es menor que 1 y x es un valor cualitativo, tenemos una magnitud cualitativa. Se interpreta como una fracción o proporción de la expresión x. Por ejemplo,


0.7*alto    0.5*joven    0.8*caliente

El factor puede afectar a cualquier cualidad, incluyendo las cualidades de verdad (V) o falsedad (F). En este caso, tenemos una magnitud de verdad cualitativa. Por ejemplo.


0.7*V       0.3*F

Factorización en variables y valores lingüísticos

Una variable lingüística (o cualitativa) x y uno de sus valores cualitativos v se representa por x/v (la particularización de x con el valor v). Por ejemplo: velocidad/alta, estatura/media, edad/joven, etc.

Factorización en conjuntos

En el caso de la relación de pertenencia de un elemento a a un conjunto C, la factorización puede afectar al elemento, al conjunto o a ambos. Hay 8 posibilidades:

`a∈C`	`f*(a∈C)`
`(f*a)∈C`	`f1(f2a)∈C)`
`a∈(f*C)`	`(f1a)∈(f2C)`
`f1(a∈(f2C))`	`f1((f2a)∈(f3*C))`

Operaciones lógicas difusas

Negación lógica difusa:
⟨( (f*x)' = (1−f)*x )⟩ ⟨( (f*x)' = f*x' )⟩

Por ejemplo, (0.7*alto)' = 0.3*alto = 0.7*bajo), suponiendo que
(alto' = bajo) y (bajo' = alto)
Suma lógica difusa:
⟨( (f1*x +/d f2*x) = max(f1 f2)*x )⟩
Producto lógico difuso:
⟨( (f1*x +/d f2*x) = min(f1 f2)*x )⟩

en donde d es el predicado “difuso” aplicado al operador suma, y max y min las funciones de máximo y mínimo, respectivamente.

⟨( max(f1 f2) = f1 ← f1>f2 →' f2) )⟩ ⟨( min(f1 f2) = f1 ← f1<f2 →' f2) )⟩

Por ejemplo:

(0.3*a +/d 0.8*a) // ev. 0.8*a (0.3*a */d 0.8*a) // ev. 0.3*a (0.3 +/d 0.8) // ev. 0.8 (0.3 */d 0.8) // ev. 0.3
Implicación lógica difusa.
En MENTAL no tiene sentido asignar un valor de verdad a la implicación porque se trata de una expresión tipo “condición → acción”. Por lo tanto, solo hay una interpretación: cuando existe la expresión de condición, se evalúa la acción. [ver Aplicaciones – Lógica – El Problema de la Implicación.]

Operaciones con conjuntos difusos

Conjunto difuso complementario:

⟨( (C('/d) = C/⟨(r*x = (1−r)*x)⟩ )⟩
Unión difusa de conjuntos:

⟨( (C1 ∪/d C2) = (C1 ∪/d C2)/g1 )⟩

siendo ( g1 = ⟨( (r1*x r2*x)↓ = max(r1 r2)*x )⟩ )

( C1 = {0.3*a 0.6*b 0.2*c} ) ( C2 = {0.5*a 0.7*b} ) (C1 ∪/d C2) // ev. (0.5*a 0.7*b 0.2*c)
Intersección difusa de conjuntos:

⟨( (C1 ∩/d C2) = (C1 ∩/d C2)/g2 )⟩

siendo ( g2 = ⟨( (r1*x r2*x)↓ = min(r1 r2)*x )⟩ )

( C1 = {0.3*a 0.6*b 0.2*c} ) ( C2 = {0.5*a 0.7*b] ) (C1 ∩/d C2) // ev. (0.3*a 0.6*b)

Otras operaciones difusas

Suma vectorial y suma vectorial difusa:

⟨( (s1 +/v s2) = ( [⌊s1↓⌋ + ⌊s2↓⌋] ) )⟩ ⟨( (s1 +/vd s2) = ( [⌊s1↓⌋ +/d ⌊s2↓⌋] ) )⟩

Ejemplos:

(g1 = (0.3*a 0.6*b)) (g2 = (0.5*a 0.7*b)) (g1 +/v g2) // ev. (0.8*a 1.3*b) (g1 +/vd g2) // ev. (0.5*a 0.7*b)
Suma matricial y suma matricial difusa (para matrices de 2 dimensiones):

⟨( (m1 +/m m2) = ( [⌊m1↓⌋ +/v ⌊m2↓⌋] ) )⟩ ⟨( (m1 +/md m2) = ( [⌊m1↓⌋ +/vm ⌊m2↓⌋] ) )⟩

Ejemplos:

( ((1 2) (3 4)) +/m ((5 6) (7 8)) ) // ev. ((6 8) (10 12)) ( ((1 2) (3 4)) +/md ((5 6) (7 8)) ) // ev. ((5 6) (7 8))

Ejemplo de sistema de control difuso: ventilador

Podemos integrar las 3 fases de un sistema de control difuso (fuzzificación, evaluación de las reglas difusas y desfuzzificación) en una sola expresión: una función de entrada (la temperatura t) y de salida la velocidad angular w del ventilador:


// función de control. Entrada: t (temperatura). Salida: w (velocidad ventilador)


//


// función auxiliar para el cálculo del factor asociado a cada tipo de temperatura


//


⟨( y(x x1 y1 x2 y2) = y1 + (y2 – y1)*(x − x1)÷(x2 − x1 )⟩


//


// valores de referencia


//


   (t1=10 t2=20 t3=30) // temperaturas


   (w1=30 w2=60 w3=120) // velocidades del ventilador


//


// reglas


//


   ( r1 =: (t/Fría → w/Mínima) )  // regla 1



   ( r2 =: (t/Templada → w/Media) )  // regla 2



   ( r3 =: (t/Caliente → w/Máxima) )  // regla 3



//


// fuzzificación: Obtención de los valores cualitativos en función de la temperatura t


//


   ( t≤t1 → (f1=1 f2=0 f3=0) )



( (t>t1 ∧ t≤t2) →

     (f1=y(t t1 1 t2 0) f2=(y(t t1 0 t2 1) f3=0)) )



( (t>t2 ∧ t≤t3) →


     (f1=0 f2=(y(t t2 1 t3 0) f3=(y(t t2 0 t3 1)) )



 ( t>t3 → (f1=0 f2=0 f3=1) )


(f1>0 → t/Fría) (f2>0 → t/Templada) (f3>0 → t/Caliente) 


//


// evaluación de las reglas


//


   (r1 r2 r3)   


//


// desfuzzificación 


//


   ( w = (w1*f1 + w2*f2 + w3*f3)÷(f1+f2+f3) )


   ¡w)! )⟩

Adenda
Teoría de la posibilidad

Zadeh “fuzzyficó” (“difusificó” o “borrosificó”) la probabilidad y la convirtió en probabilidad difusa, una generalización de la teoría de la probabilidad que denominó “teoría de la posibilidad”. Ambas teorías (la lógica difusa y la probabilidad difusa) tratan de la incertidumbre. Hay 3 tipos de incertidumbre:

La aleatoriedad de los sucesos. Por ejemplo, lanzar un dado y que salga el 6. Este campo es el de la probabilidad.
La imprecisión, causada por la vaguedad o la ambigüedad. Por ejemplo, los predicados difusos alto, bajo, rápido, lento, viejo, joven, etc. que inducen conjuntos difusos.
Una aleatoriedad con imprecisión. Por ejemplo, “que llueva o no mañana”, en la que aparece aleatoriedad (que llueva o no) e imprecisión (hay grados de lluvia: lluvia fina, tormenta, etc.).

Esta última alternativa es la más genérica y es la que estudia la teoría de la posibilidad.

MIQ (Machine Intelligence Quotient)

Los sistemas difusos emulan la mente humana, por lo que Zadeh propuso el concepto de “cociente intelectual” de un sistema o de una máquina. MIQ es una marca registrada de Zadeh.

Aplicaciones de la lógica difusa

La lógica difusa ha tenido un enorme éxito, por su simplicidad conceptual, su facilidad de aplicación y su efectividad. Aunque la intención inicial de Zadeh fue crear un formalismo para el razonamiento humano utilizando conceptos imprecisos, causó cierta sorpresa el que el éxito llegara en el campo del control automático de sistemas y procesos.

Los sistemas difusos de control (o de control difuso) son más eficientes y consumen menos energía que los sistemas clásicos. En la actualidad, una gran cantidad de patentes de productos se basan en la lógica difusa.

La primera aplicación industrial fue el control de un horno de cemento en Dinamarca, en 1980 realizada por F.L. Smidth&Co.

En EE.UU., los sistemas difusos fueron inicialmente ignorados porque se asociaban a la inteligencia artificial, un campo falto de credibilidad tras la decepción de las expectativas creadas, especialmente en los años 1980’s.

Fueron los japoneses los que primero se interesaron en la lógica difusa, aplicándola a sistemas industriales y de consumo:

La empresa Hitachi, en 1985, lo aplicó a los sistemas de control de los trenes del metro de la ciudad japonesa de Sendai, en el tema de la aceleración, desaceleración (frenado) y parada. El sistema tiene 59 reglas. Todas se disparan en cierto grado en función de la velocidad. La conducción resultó ser más suave que todas las conocidas anteriormente, tanto humana como mecánica. La precisión de la frenada fue de 7 cm, mientras que la realizada por un conductor suele superar los 20 cm. Las aceleraciones y desaceleraciones resultaron ser mucho más suaves. El número de cambios de marcha se redujo a un tercio de los de la conducción humana o de los controlados informáticamente por sistemas no difusos. Todo ello redundó, además, en un ahorro del 10 % de energía. El sistema de control se inauguró en 1987. Dado su éxito, pronto el Ayuntamiento de Tokio contrató a Hitachi para que instalase también sistemas difusos de control en el metro de Tokio.
En 1987 se aplicó para el control fuzzy en un experimento de “pendulo invertido”, un problema clásico de control en el que un vehículo trata de mantener el equilibrio de un mástil mediante un gozne vertical, moviéndolo hacia adelante y hacia atrás.
Otras aplicaciones japonesas de control difuso fueron: cámaras fotográficas de enfoque automático y de estabilización de la imagen; televisiones que ajustan el volumen y la luminosidad según el ruido y la luz ambiental; lavadoras inteligentes que seleccionaban el mejor programa de lavado según la cantidad de ropa y el grado de suciedad; microondas que se ajustan según la humedad ambiente; sistemas de aire acondicionado, que regula la temperatura en función de la temperatura ambiente; duchas que controlan la temperatura mediante combinación de agua fría y caliente; robots de fabricación; etc.

Otras aplicaciones, en USA y Europa, son: motores eléctricos de eficiencia energética; atraque (docking) espacial automática; control de compuertas en plantas hidroeléctricas, sistemas expertos; sistemas de auto−aprendizaje; cambios de marcha automáticos, control de frenado ABS y control de crucero en automóviles; reconocimiento de patrones; reconocimiento de escritura manuscrita; robots controlados por voz; control de tráfico; centrales térmicas; visión por ordenador (seguimiento de objetos mediante cámara de video); sistema de control de vehículos (aviones, ascensores, helicópteros); etc.

La difusión de la lógica difusa

En la actualidad, la lógica difusa es un campo de investigación muy amplio e importante, tanto a nivel teórico como práctico. Existen muchas publicaciones especializadas. Destacan dos revistas: "fuzzy Sets and Systems" y "IEEE Transactions on fuzzy Systems". Se organizan congresos internacionales. Hay varias asociaciones. En España está la Asociación Española de Lógica Borrosa.

En el impulso a la lógica difusa sobresalen los japoneses. El gobierno japonés ha participado en la creación de dos centros de investigación: LIFE (Laboratory for International fuzzy Engineering), creado en 1985, y el FLSI (fuzzy Logic Systems Institute), creado en 1990. Ambos centros organizan congresos cada dos años.

Críticas a la lógica difusa

Las ideas no ortodoxas de Zadeh fueron acogidas inicialmente con cierto escepticismo, pero fueron progresivamente ganando en aceptación hasta hoy día, en que el éxito se considera total y absoluto. Pero en el camino hubo muchas críticas:

Críticas generales:

El concepto de “verdad parcial” ha sido objeto de controversia. Algunos lógicos sostienen que la verdad es algo absoluto, que no tienen grados.
La pertenencia parcial a un conjunto o categoría es un tema subjetivo, pues no hay forma de determinar objetivamente los valores de pertenencia parcial. Por ejemplo, para una persona una estatura de 1.65 metros puede ser baja y para otra puede ser normal (ni alta ni baja).

Críticas de autores:

Quine una vez describió las alternativas a la lógica bivalente como “desviadas” y calificó cierta literatura sobre lógica difusa como “irresponsable”.
Dennis Lindley, un estadístico bayesiano, afirmó: “La probabilidad es la única sensible descripción de la incertidumbre y es adecuada para todos los problemas que impliquen incertidumbre. Todos los otros métodos son inadecuados”.
”Borrosidad es probabilidad disfrazada. Yo puedo diseñar un controlador con probabilidad que pueda hacer las mismas cosas que se pueden hacer con lógica difusa” (Mylon Tribus, al saber de su aplicación al metro de Sendai, Japón).
“El peligro de la lógica borrosa es que da alas a esa suerte de pensamiento impreciso que nos ha traído tantos problemas. La lógica borrosa es la cocaína de la ciencia” (William Kahan).
“La borrosidad es una suerte de permisividad científica. Tiende a acabar en eslóganes socialmente atractivos que no van acompañados de la disciplina del duro trabajo científico y de la observación paciente” (Rudolf Kalman).

La lógica difusa e Internet

La lógica difusa es muy adecuada para representar el conocimiento, especialmente en Internet. A iniciativa del propio Zadeh, en 2001 tuvo lugar el primer encuentro sobre lógica difusa e Internet (FLIT 2001), celebrado en la Universidad de Berkeley. Las ponencias están publicadas en la web de BISC. La idea principal es usar técnicas de Soft Computing para representación del conocimiento, categorización de la información, búsqueda difusa, agentes inteligentes autónomos, minería de datos, etc.

Bibliografía

Dubois Didier; Prade Henry. fuzzy numbers. An overview. In: Analysis of fuzzy Information, 1:3−39, CRC Press, 1987.
Freilberger, Paul; McNeill, Daniel. Fuzzy Logic. Simon & Schuster, 1993.
Glöckner, Ingo. Fuzzy Quantifiers. A Computational Theory. Springer, 2006.
Kaufmann, Arnold; Gupta, Madam M. Introduction to Fuzzy Arithmetic: Theory and Applications. Van Nostrand Reinhold, 1991.
Klir, George J.; Clair, Ute St.; Yuan, Bo. Fuzzy Sets Theory. Foundations and Applications. Prentice−Hall, 1997.
Kosko, Bart. El futuro borroso o El cielo en un chip. Crítica, 2010.
Kosko, Bart. Fuzzy Engineering. Prentice−Hall, 1997.
Kosko, Bart. Fuzzy Thinking. The New Science of Fuzzy Logic. Flamingo, 1994.
Kosko, Bart. Fuzzy Engineering. Prentice Hall, 1996.
Mattila, Jorma K. Text Book of Fuzzy Logic. Art House, 1998.
McNeill, Daniel. Fuzzy Logic: The Revolutionary Computer Technology That Is Changing Our World. Simon & Schuster, 1994.
Nguyen, Hung T.; Walker, Elbert A. A First Course in Fuzzy Logic. Chapman and Hall/CRC, 2005.
Ross, Timothy J. Fuzzy Logic with Engineering Applications. Wiley, 2010.
Sangalli, Arturo. The Importance of Being Fuzzy. Princeton University Press, 1998.
Trillas Ruiz, Enric; Alsina, Claudi; Terricabras, Josep Maria. Introducción a la lógica borrosa. Ariel, 1996.
Trillas Ruiz, Enric; Cubillo Villanueva, Susana. Primeras lecciones de lógica borrosa. Universidad Politécnica de Madrid, Facultad de Informática, Departamento de Publicaciones, 1999.
Yager, R.R. Quantified Propositions of a Linguistic Logic. International Journal of Man−Machine Studies, vol. 19, pp. 195−227, 1983.
Yen, John; Langari, Reza. Fuzzy Logic: Intelligence, Control, and Information. Prentice Hall, 1998.
Zadeh, Lofti A. Fuzzy sets. Information and Control 8(3): 338−353, 1965.
Zadeh, Lofti A. ¿Qué es Soft Computing? Internet, 1994.
Zadeh, Lofti A. Fuzzy Algoritms. Information and Control, vol. 12, pp. 94−102, 1968.
Zadeh, Lofti A. A Computational Aproach to Fuzzy Quantifiers in Natural Languages. Computer Mathematics with Applications, vol. 9, pp. 149−183, 1983.
Zadeh, Lofty A. A rationale for Fuzzy control. J. Dynamic Systems, Measurement and Control, vol. 94, series G, pp. 3−4, 1972.
Zadeh, Lofti A. Outline of a new approach to the analysis of complex systems and decision processes. IEEE Transaction Systems, Man & Cybernetics, vol. SM^C−3, no. 1, pp. 28−44, 1973.
Zadeh, Lofti A. Fuzzy logic. IEEE Computer Magazine, pp. 83−93, April 1988. Disponible en Internet.